Zero Knowledge Proofs / Secure Computing

Notes and reference for some intro crypt + zero knowledge. IN PROGRESS.

1. Intro

AI inference services require blind trust. Key security risks are privacy of the user’s input and integrity of the server’s output. Ideally, we want private and verifiable computation. The user should send an encrypted question to a trustworthy server which computes and the encrypted response. The user can then decryp the response and verify that it is the intended output of the model, without learning anything else about the model.

Three key capabilities to learn about:

• zero knowledge proofs
• succinct (non-interactive) proofs
• fully homomorphic encryption.

Zero Knowledge Proofs

What is a proof system? The prover has some claim and creates proof $\pi$. This proof is sent to the verifier, who will run an algorithm to either accept or reject this proof.

In a zero knowledge proof, a prover wants to convince a verifier that a statement is true without revealing secret evidence.

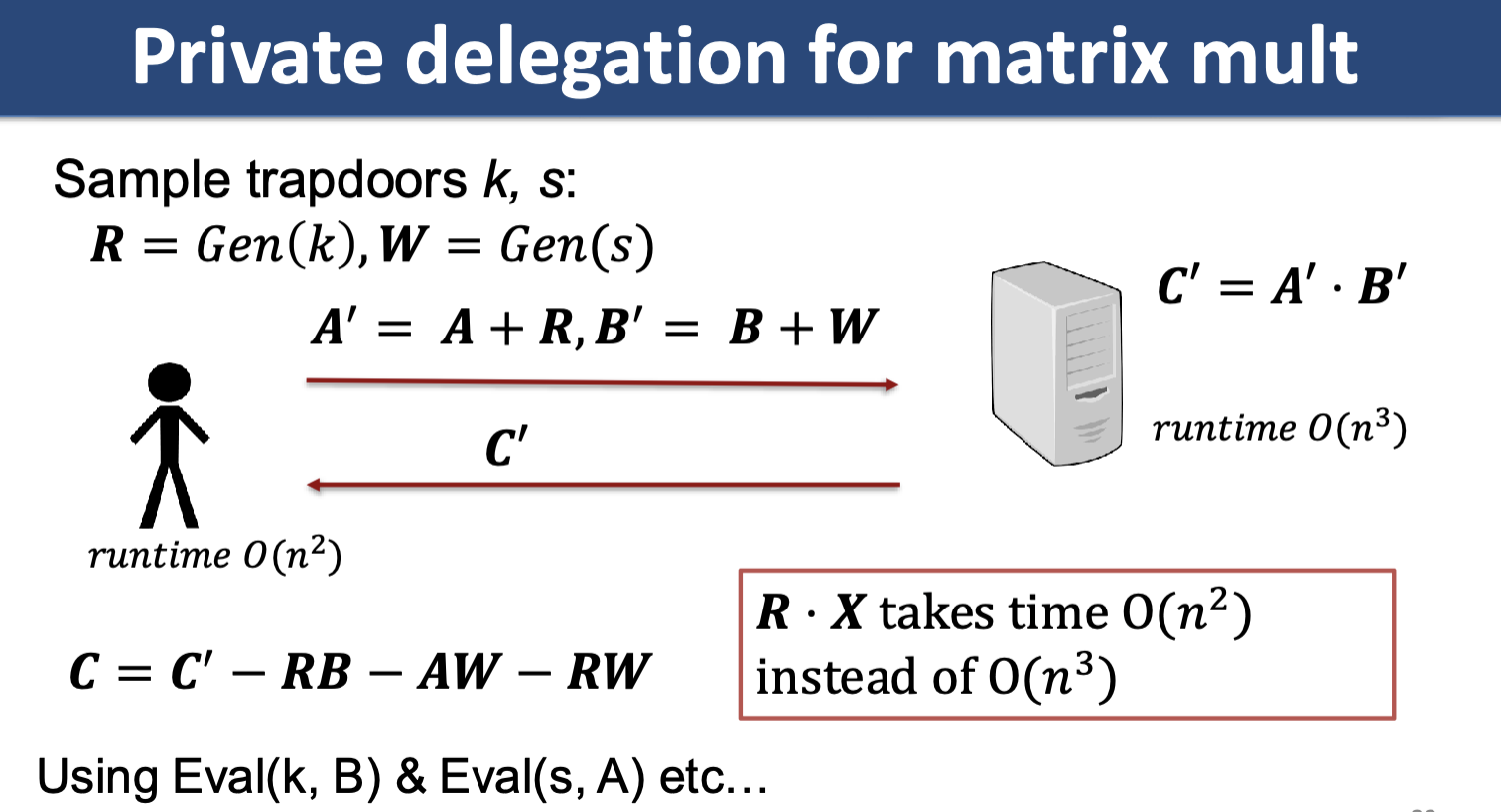
2. Trapdoor Matrices

Frievald’s Algorithm

FACT: For nonzero $M \in \F^{n\times n}$ and uniform random $r \in \F^n$,

$$\P(M*r =0) \leq 1/| \F |.$$

Algorithm: we want to multiply two matrices $A,B \in \F^{n \times n}$ and check that the matrix returned, $C$, is correct.

• sample random $r \in \F^n$
• server does $C = A*B$, returns to us.
• check $A*(B*r) = C*r$
• if yes, accept

Now, check with a matrix:

• sample random $R \in \F^{n \times k}$
• check $A*(B*R) = C*R$
• if yes, accept

Pseudorandom matrix

Matrix generation algorithm given a key $k \in \{0,1\}^\lambda$.

$$R \leftarrow \text{Gen}(k)$$

defines a pseudorandom family if, for uniform random key, no algorithm (without the input $k$) running in time $T$ can distinguish the matrix $R$ from random with probability better than $T/2^\lambda$.

Trapdoored pseudorandom matrix

$R \leftarrow \text{Gen}(k)$ is a pseudorandom $n \times n$ matrix and there is a special algorithm

$$y \leftarrow \text{Eval}(k,X)$$

that given any $X \in \F^n$ returns $y = R*X$ and $\text{Eval}$ runs in time $O(n^2)$.

3. Collision Resistance, Hardness

4. Private, verifiable computation (preliminaries)

Previously: DL and collision-resistant hash from DL

Groups of unknown order

A group where the order is computationally hard to compute, defined by group sampling alg

$$<\mathbb{G}>, n \leftarrow \text{GGen}(1^\lambda)$$

for $<\mathbb{G}>$ a succinct (size polynomial in $\lambda$) description of a group $\mathbb{G}$ and $n$ an upper bound on its order.

The hidden order assumption holds for $\text{GGen}$ if for any polynomial time algorithm $A$ and distribution:

• $<\mathbb{G}>, n \leftarrow \text{GGen}(1^\lambda)$
• $g \leftarrow \mathbb{G}$ a uniformly distributed group element
• $a \leftarrow A(g, <\mathbb{G}>, n)$

$$\P [g^a = 1 ] < \text{negl}(\lambda).$$

RSA assumption (fill in)

GUO with trusted setup: the algorithm $\text{GGen}$ is allowed to randomly generate secret values that are discarded.

Ex: $\text{GGen}$ samples secret primes $p,q$ and outputs $N = p*q$ defining the group $\mathbb{Z}^*_N.$ This group has order $(p-1)(q-1)$, which is easy to compute if $N$ can be factored.

Collision resistant hash from GUO

• setup: $\mathbb{G} \leftarrow \text{GGen}(\lambda),$ and $g \leftarrow \mathbb{G}$.
• hash function: input $x \in \mathbb{Z}$ return $g^x$.

Collision-resistant based on hidden order assumption: if $g^x = g^y$ for $x \neq y$ then $g^{x-y} = 1$.

Statistical distance

The statistical distance between random variables $X, Y$ over a finite domain $D$ is :

$$\Delta(X,Y)= \sum_{\alpha \in D} \frac{1}{2}|P(X=\alpha) - P(Y=\alpha)|.$$

Sequences of random variables $(X_n), (Y_n)$ are statistically indistinguishable if

$$\Delta(X_n, Y_n) = 1/ 2^n.$$

Sequences $(X_n), (Y_n)$ on the same domain $D$ are computationally indistinguishable if for any polynomial time algorithm $A$ that receives an input $x \in D$ and outputs $0$ or $1$:

$$|P(A(X_n) = 1) - P(A(Y_n) = 1)| = 1/2^n.$$

Learning parity with noise

The LPN assumption over a field $\mathbb{F}$ has a dimension parameter $k$, noise rate $\epsilon$, and number of samples $N$.

The assumption is that a list of $n$ samples of the form $(r_i, r_i * s + e_i)$ is computationally indistinguishable from a list of $n$ samples of the form $(r_i, u_i)$ where

• $s,r_i \in \mathbb{F}^k$ and $u_i \in \mathbb{F}$ are uniform
• $e_i$ is 0 with probability $1 - \epsilon$ and otherwise uniform in $\mathbb{F}$.

Pseudorandom matrix from LPN

$$R = A*S + E$$

where $A \in \mathbb{F}^{n \times k}$ and $S \in \mathbb{F}^{k \times n}$ and all entries of $E$ are sampled as $e_i$ on previous slide.

Each entry of $R$ has the form $r_{ij} = a_i * s_j + e_{ij}.$

For each $s_j$ get $n$ samples of the form $a_i * s_j + e_{ij} \approx u_{ij}.$

Languages, NP, and P

A language is a subset of strings $L \subset \{0,1\}^*.$

A language $L$ is in NP if there exists a deterministic polynomial times algorithm $D$ and polynomial $q(\cdot)$ such that:

• for any $x \in L$ there exists a “witness” $w$ of length $q(|x|)$ such that $D(x,w) = 1.$
• if $x \notin L$ then $D(x,w)=0$ for any $w$ of length $q(|x|)$.

A language $L$ is in P if there exists a polynomial time algorithm $S$ such that $S(x) =1$ if and only if $x \in L$.

NP relations

A binary relation $R$ is a subset of $\{0,1\}^* \times \{0,1\}^*.$ The language $L_R$ of a binary relation $R$ is the set

$$\{x \in \{0,1\}^* \text{ : there exists } w \text{ s.t. } (x,w) \in R \}.$$

$R$ is called an NP relation if the language $L_R$ is in NP.

How to represent algorithms?

• Turing machines (not useful for proof systems)
• Arithmetic circuit families
• RAM programs

Arithmetic circuits

Fix a finite field $\mathbb{F} = \{0, ..., p-1\}$ for some prime $p>2.$

An arithmetic circuit is defined $C: \mathbb{F}^n \rightarrow \mathbb{F}$. It is a directed acyclic graph (DAG) where internal nodes are labeled as $+, -,$ or $\times$. Inputs are labeled $1, x_1, ..., x_n$. This defines an $n$-variate polynomial with an evaluation recipe.

$|C|$ usually denotes the number of multiplication gates in $C$.

5. Private, verifiable computation

Representing algorithms (above).

Boolean circuits can be represented as arithmetic circuits over $\mathbb{F}_p$:

• $AND(x,y)$ encoded as $x*y$
• $OR(x,y)$ encoded as $x+y - x*y$
• $NOT(x)$ encoded as $1-x$

Proof verification asymptotically faster than program evaluation = verifiable computation.

Sound: infeasible to produce valid proof if prover doesn’t know program $w$ Zero knowledge: proof doesn’t reveal anything about the program $w$

Proof system syntax

• A transcript is a recording of messages between prover and verifier
• Prover algorithm:
  • algorithm $\text{Prove}(x,w,tr,st) \rightarrow (m,st')$ takes input $x$ and witness $w$, internal state $st$, transcript $tr$, and produces an updated state and next message, which is sent to verifier.
• Verifier algorithm:
  • algorithm $\text{Verify}(x, tr, st) \rightarrow (m, st')$ takes only input $x$, internal state $st$, transcript $tr$, and produces and updated state and next message, which is sent back to prover.

Completeness property

Notation: $< P(x,w), V(x)>$ denotes output of verifier on interaction with prover for input $x$ and witness $w$.

For all $(x,w)$ s.t. $C(x,w) = 0$, there is a probability 1 that $<P(x,w), V(x)> = 1$.

Soundness property

Notation: $<A(x,w), V(x)>$ the output of verifier on interaction with an adversarial prover algorithm $A$ for input $x$ and witness $w$.

For any $x$ where there does not exist $w$ such that $C(x,w) = 0$ and any polynomial time algorithm $A$, the probability that $<A(x,w), V(x)> = 1$ is boundeed by $\text{negl}(|x|).$

Weaker SNARKS with trusted setup

We believe there’s some trusted party that creates the parameters and then disappears. Risky because a broken trusted setup is very bad.

Sometimes we can use multi-party trusted setup.

Types of pre-processing setup:

$$\text{Setup}(1^\lambda, C) \rightarrow \text{public parameters}(pk,vk).$$

• trusted setup per circuit
• universal trusted setup (secret part of setup not specific to circuit)
• updatable universal trusted setup (public parameters can be updated by anyone)
• transparent (setup does not use secret data at all)

Completeness property with setup

<P(pk, x,w), V(vk, x)> denotes output of verifier on interaction with prover for input $x$ and witness $w$.

For all $(pk, vk) \leftarrow \text{Setup}(1^\lambda)$ (finish line from slides)

Soundness property with setup

from slides

Knowledge & Soundness

What does it mean to have knowledge?

Soundness is a aproperty of a proof system that ensures cheaters cannot convince the verifier of a false statement. Soundness $\implies$ if the prover succeeds, there must exist a witness (except with very small probability). This is too weak for some applications.

Knowledge soundness captures the property that the prover must somehow “know” the witness $w$ in order to succeed in the protocol.

A protocol is knowledge sound if there exists an extractor algorithm E that can obtain the witness w from any successful prover (informal).

The extractor:

• E can run A for any number of steps
• rewind A to a previous state
• re-run A on different inputs.

For every adversarial prover $A$ and input $x$ that causes verifier to accept with non-negligible probability, $E$ outputs $w$ such that $C(x,w) = 0$ with high probability.

6. Proofs/Args of Knowledge, Zero Knowledge

Recap on knowledge soundness.

Proofs and arguments of knowledge

Oracle access to prover: Adversarial prover A is a stateful process that interacts with the verifier (internally runs a modified prover algorithm to get each next message).

If E is an algorithm that has oracle access to A then:

• E can simulate interaction with the verifier for some number of steps, obtaining each message that A sends, but not internal state
• E can rewind to A to a prior internal state, and redo the simulation on new inputs

A protocol has $\delta(\lambda)$ knowledge error if

• There exists a polynomial $P$ and extractor $E$
• $E$ given oracle access to any adversary $A$ and input $x$ s.t. $|x| \geq \lambda$ and $\P [ <A(x,w), V(x)> = 1] = \epsilon.$
• $E$ runs in time $P(|x|)/\epsilon$ and outputs $w$ such that $C(x,w) = 0$ with prob at least $1 - \delta(\lambda) / \epsilon$.

Protocol is called proof of knowledge if $\delta(\lambda)$ negligible.

Argument of knowledge: same definition as proof of knowledge, except extractor is only guaranteed to succeed for polynomial time adversary $A$.

Succinctness, SNARKs

An interactive argument for circuit $C$ with $n$ gates and setup parameter $\lambda$ is succinct if:

• the total communication between prover and verifier over all rounds is $O(\text{polylog}(n), \lambda)$
• the cumulative verifier runtime over all rounds is $O(\text{polylog}(n), \lambda)$.

Succinct noninteractive arguments abbreviated SNARK. Zero-knowledge SNARK abbreviated zkSNARK.

The differences between SIA and SNARK:

• Non-interactive: There is only one message from the prover to the verifier, a single short proof
• Knowledge soundness: If the proof is accepted, then there is a valid witness that can be extracted (not just soundness, but proof of knowledge).

Zero knowledge

• There is a simulator, Sim, that is given oracle access to any adversarial verifier $V$.
• Sim receives the input $x$ but not the witness $w$.
• It runs in polynomial time and produces a simulation of the transcript between prover and verifier.
• The simulated transcript is indistinguishable from a real transcript.

Non-interactive zero knowledge

Sim can simulate the proof $\pi$ without the witness $w$. Therefore, the proof reveals nothing about $w$ that an observer did not already know before seeing $\pi$. How?

Clearly the Sim cannot produce a convincing proof $\pi*$, otherwise soundness breaks. Then how can it simulate?

• The proof $\pi*$ is not convincing because Sim can “cheat” on the setup.
  • It generates parameters $pk*$ and $vk*$ AFTER creating $\pi*$, or by using knwoledge of the secret in its simulation of a trusted setup.
• In other words, Sim has power that the real prover doesn’t have.

7. Polynomial Commitments and Classical ZKP

A polynomial commitment scheme (PCS) provides

• A collision-resistant hash function for polynomials over $\mathbb{Z}_p$
• A special proof system for a polynomial input to the hash function

A hiding/ZK PC is:

• Binding: Once you commit to a polynomial, you cannot later change your mind and claim a different polynomial that matches some evaluations.
  • This is like “soundness”–it prevents cheating.
• Hiding (or Zero-Knowledge): The commitment does not reveal information about the polynomial except what you later explicitly reveal. This is the “privacy” property.

ZKP of DL

Problem: Given group elements $g, h \in \mathcal{G}$ in a group of prime order $p$, provide a ZK PoK of a witness $x \in [0,p)$ such that ß$g^x = h$.

Prover message: sample $r \in [0, p-1]$ and send $R = g^r$

Verifier challenge: sample $c \in [0, 2^\lambda)$ and send $c$

Prover response: send $z = r+x * c \mod p$

Verifier decision: accept iff $R * h^c = g^z$

Three round protocol of this form has a special name, the sigma protocol.

• Completeness: The protocol is perfectly complete.
• What about soundness and zero knowledge?
  • We only have “honest verifier zero knowledge”

Special Soundness

A sigma protocol is special sound if from any two transcripts $(m,c,z)$ and $(m, c', z')$ where $c \neq c'$ there is a polynomial time extractor that computes a witness.

Honest verifier ZK

Assuming the verifier behaves honestly, we can simulate:

Simulator:

• sample random $z$ and random $c$
• set $R = g^z / h^c$
• return $(R,c,z)$

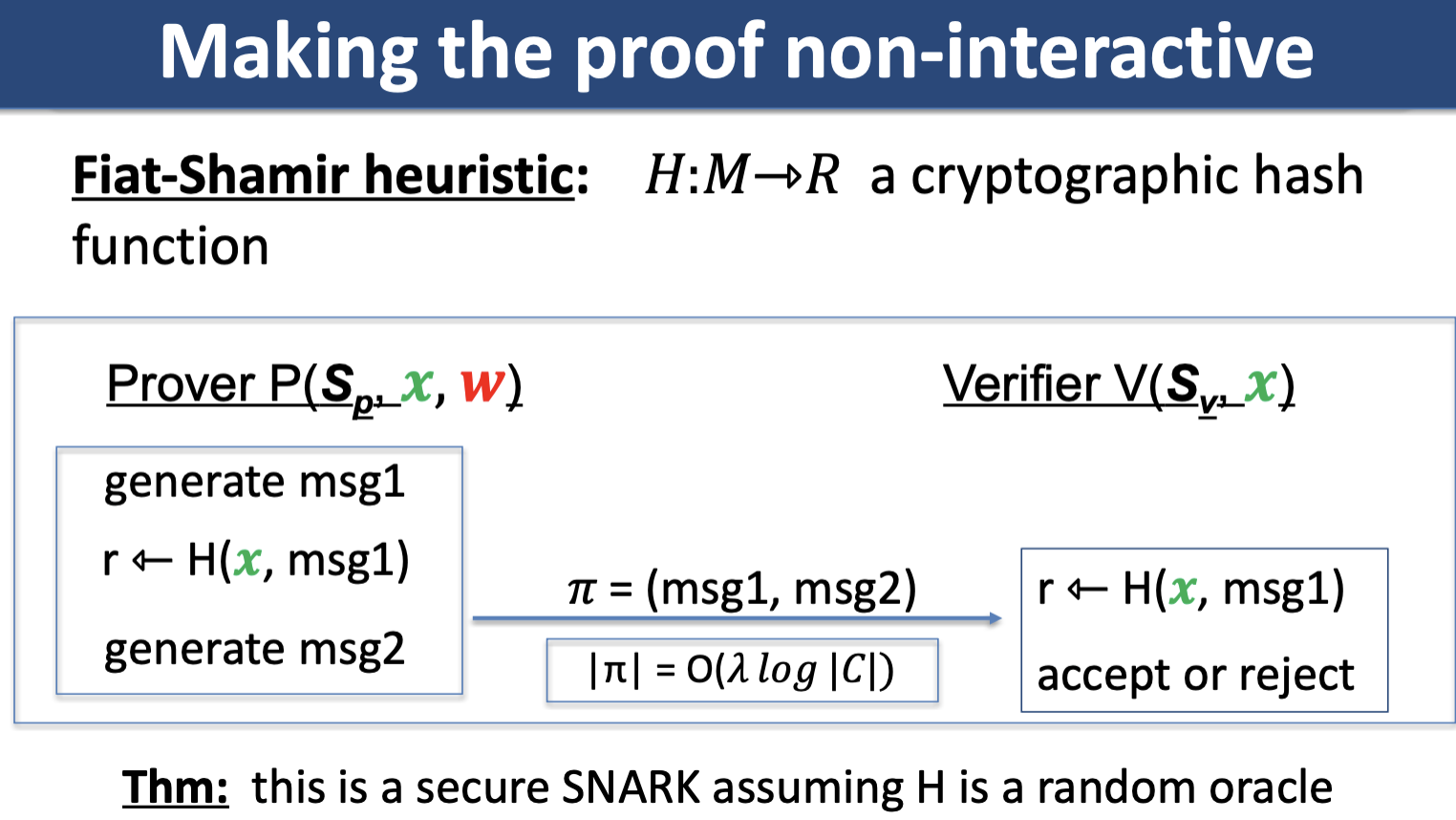
Fiat-Shamir Transform

A technique for taking an interactive PoK and creating a digital signature based on it. For sigma protocol, Fiat-Shamir transformation says instead of having verifier send a random challenge value to the prover, the prover can compute this value themselves by using a random function, leading us to the idea of random oracles.

Random oracle model

In the random oracle model, both prover and verifier algorithms have oracle access to a completely random function $H$.

The random oracle model enables constructions of non-interactive proofs.

How can a simulator simulate a non-interactive proof without knowing a witness? In the random oracle model, the simulator can cheat by “re-programming” the random oracle at points (but must preserve the distribution of random oracle, e.g. re-program a point to uniform random output).

HVZK to ZK via Fiat-Shamir Transform

Schnorr Signatures

Apply Fiat-Shamir to ZKPoK of DL:

Public key: $PK = g^{sk}$ where $sk \in [0,p)$

Signature on message m: $(R,z)$ s.t. $g^z = R*PK^c$ where $c = H(m, PK, R)$.

Group homomorphism

A group homomorphism is a function $f : \mathbb{G} \rightarrow \mathbb{H}$ that satisfies $f(g_1 \cdot g_2) = f(g_1) * f(g_2)$ for all $g_1, g_2 \in \mathbb{G}$.

In additive notation, this is linearity:

$$f(g_1 + g_2) = f(g_1) + f(g_2).$$

Correlation intractability

A hash function family with sampling algorithm $\text{Gen}(1^\lambda)$ is correlation intractable for a binary relation $R$ if for all polynomial time algorithms $A$ and the following distribution:

• $H \leftarrow \text{Gen}(1^\lambda)$
• $x \leftarrow A(1^\lambda, H)$

$$P(R(x, H(x)) = 1) < \text{negl}(\lambda).$$

CI and Fiat-Shamir

A hash family is correlation intractable if it is correlation intractable for all binary relations.

Knowledge in Random Oracle Model

A Q-query random oracle algorithm is an algorithm with oracle access to random oracle $H$ that makes at most $Q$ queries to $H$. An RO protocol is a noninteractive protocol between random oracle algorithms.

8. More Polynomial Commitments + Classical ZKPs

FS transform of Sigma Protocols

Multiround Special Soundness

$k$-ary special soundness: given $k$-ary forking tree of proof transcripts for $x \in L_R$, there is a polytime algorithm that extracts a witness $w$ s.t. $(x,w) \in R$.

Simple PCP-based SNARK (Kilian, Micali)

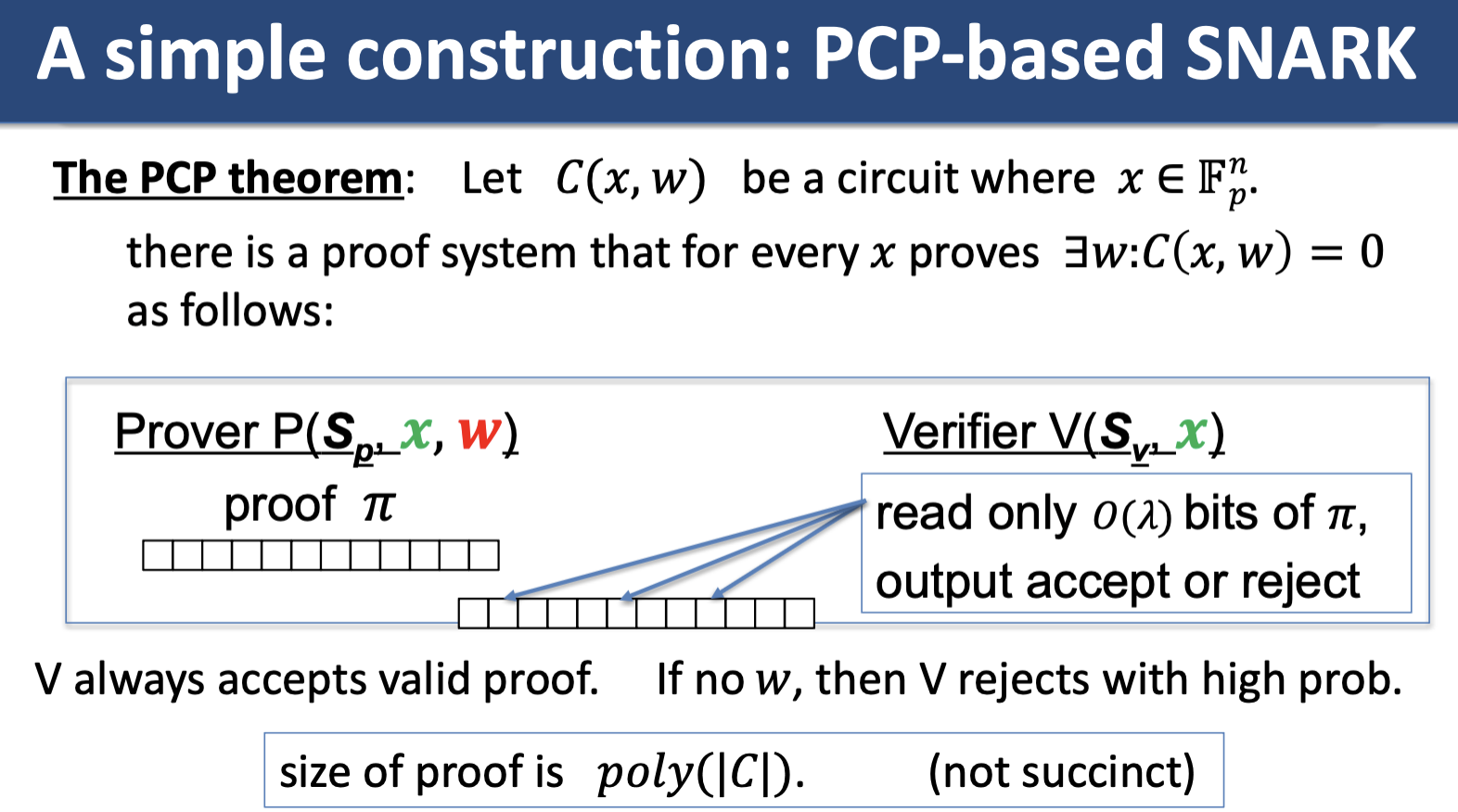
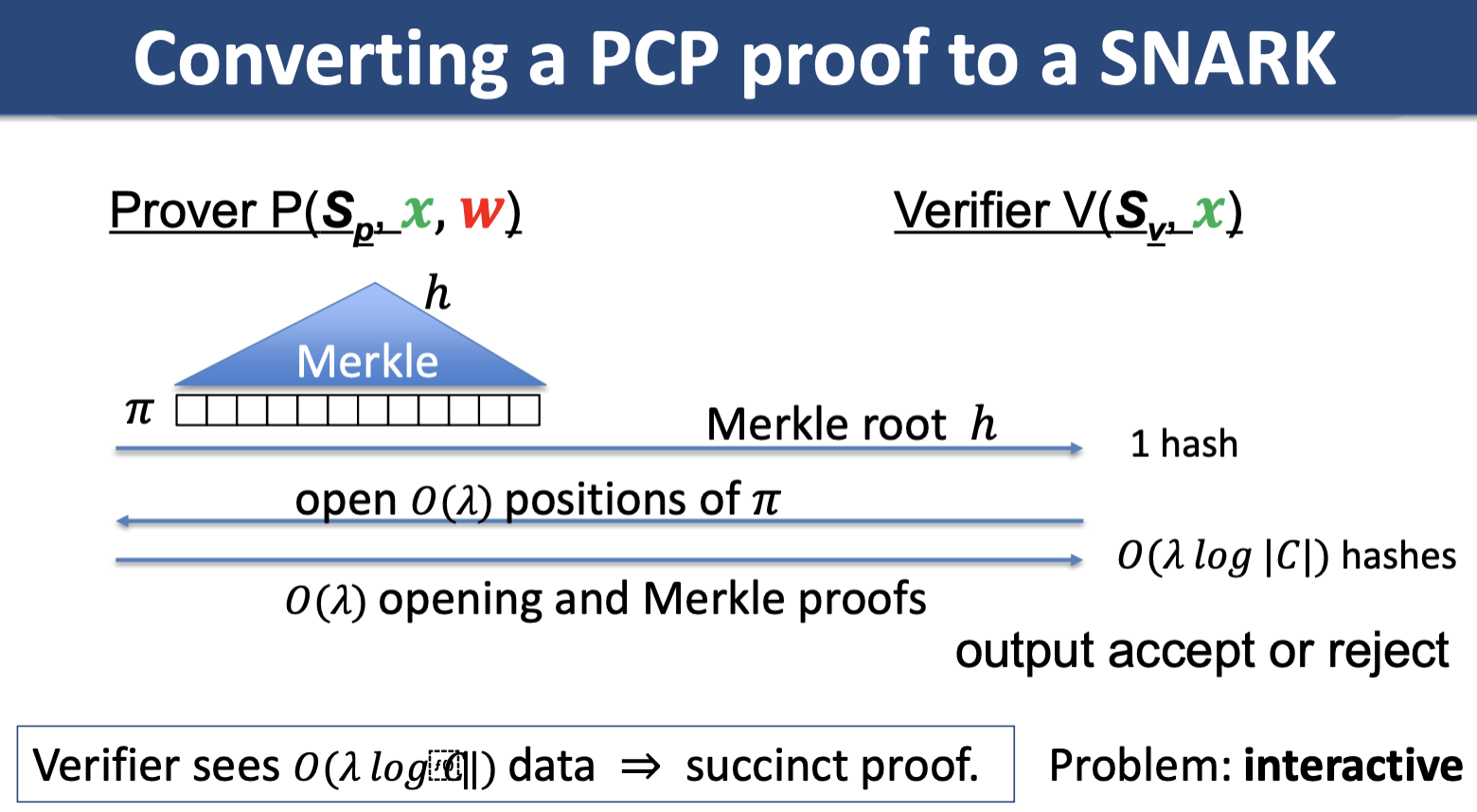
Unfortunately, this method is impractical/the prover time is very high. Later: more efficient constructions, constructions that do not require random oracles.

9. Classical Succinct Proofs

None of the classical proofs examined previously have been succinct (communication has thus been proportional to size).

Recall PoK for DL: I know $x$ s.t. $g^x = y$ over $\G$. Send $g^r$, return $c$, send $z = r + c$. Size of communication same as size of witness $x$.

Consider $x_1, ..., x_n$ s.t. $\prod g_i^{x_i} - y$. A protocol with only $O(\log n)$ bits of communication?

As with Fiat-Shamir in PoK for DL, we can do something analogous for this situation.

Generalizing sigma protocols: Recall sigma protocol for PoK HPI (homomorphism preimage). We have a $f$ a homomorphism, $f: \Z_p \rightarrow \G$ s.t. $x \mapsto g^x$. Generalize mapping from any group $H$ to $G$. Prover sends $f(r)$, verifier returns $c$, prover sends back $f = r+ cx$. Verifier checks that $f(z) = f(r) * f(x)^c$ (for $*$ the group operation).

The problem we’ve posed above is ParseError: KaTeX parse error: Undefined control sequence: \righarrow at position 11: f: \Z_p^n \̲r̲i̲g̲h̲a̲r̲r̲o̲w̲ ̲\G, e.g. with our multiple $x_i$ values we’re mapping vector $x \mapsto g^x$. Check $\prod g_i^{z_i} = (\prod g_i^{r_i}) * y^c$ for $*$ the group operation.

This is not succinct!

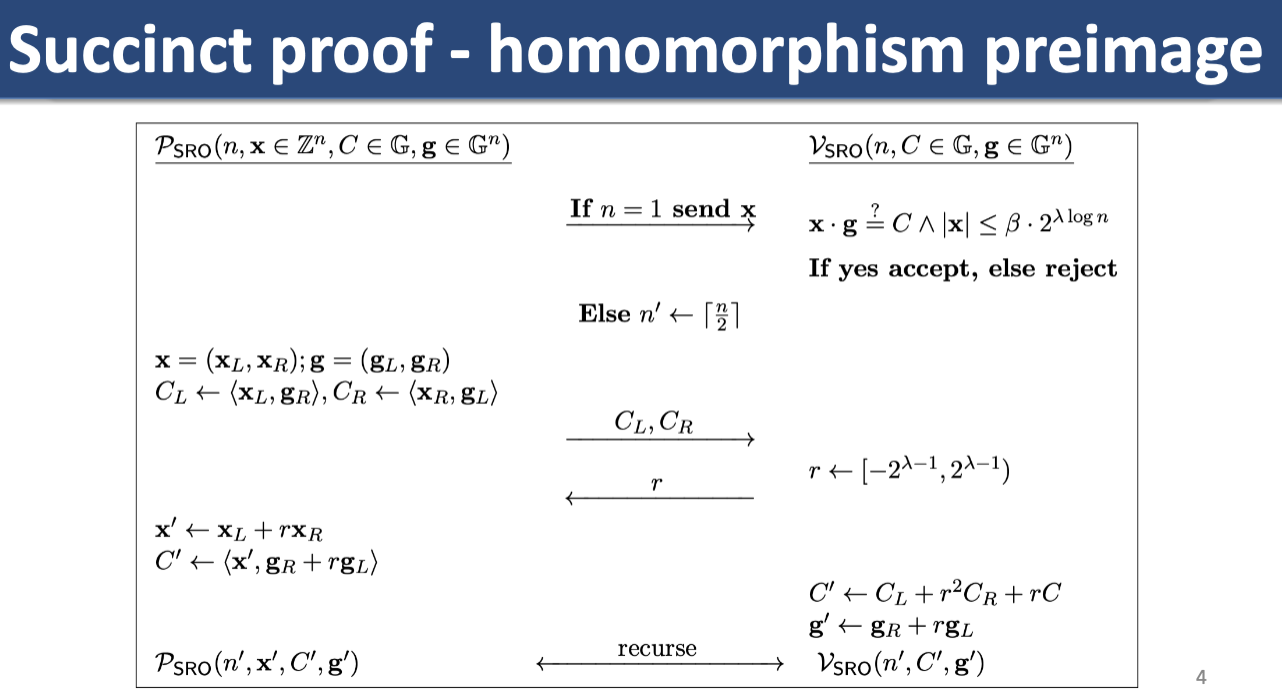
There are $log_2 (n)$ rounds (first round start with $n$, cut in half each round until $n=1$). In each round, we send two group elements $C_L, C_R$, so total communication $2 log_2(n)$.

Recal Multiround Special Soundness (Lec 8). $k$-ary special sound $\mu$ round protocol is knowledge sound for const $k$ and $\mu \in O(\log |w|)$.

10. SNARK Compilers

Compilation paradigm for SNARKs today: arithmetization -> information theoretic pf system -> SNARK.

Interactive Oracle Proofs

Pf systems today generally not built from probabilistically checkable proofs (PCPs) in the classical sense, computationally infeasible (1 round, oracle access to pf).

PCP: 1-round oracle proof, where prover sends poly sized string $\pi$, and verifier has oracle access to query locations of $\pi$ without reading whole string.

IOP: interactive oracle proof, multi round. Verifier receives new pf strings each round and has oracle access to all pf strings received.

R1CS: we have matrices $A,B,C \in \F^{m \times (n+1)}.$ Input $z = (1,x,w)$ over $\F^{n+1}.$ R1CS program accepts $(x,w)$ iff

$$(A*z) \odot (B * z) = (C*z)$$

for $\odot$ component wise product (Hadamard).

Linear PCP: PCP is a fn $f_\pi: \F^n \rightarrow \F$. Equivalent:

• pf is vector $\pi$ over the field
• oracle receives query $q$ returns $<\pi,q>.$

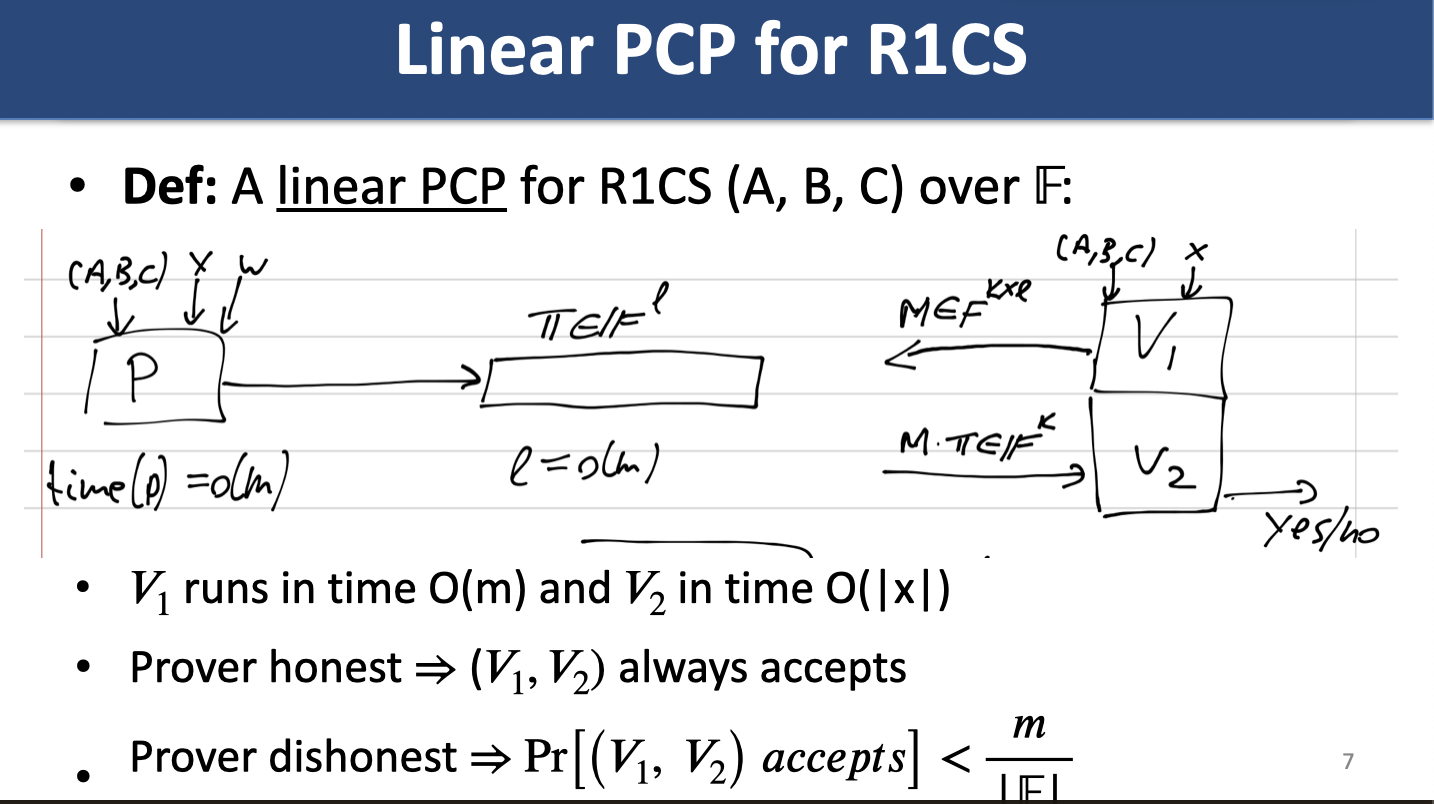
Ishai, Kushilevitz, Ostrovksy '07 show 4 round linear PCP with linear homomorphic encryption as compiler can convert linear PCPs into SNARKs.

Efficiency of IOPs

• Multiple rounds allow for great efficiency gains over classical PCPs
• Lightweight compilation (Merkle trees, hash functions) compared to linear PCP.

Some modern proof systems building SNARKs off of IOPs,

• STARK (BBHR18)
  • uniform programs (many reps fo small unit)
  • $O(\log^2 n)$ arg size, fast oepratioins
  • sublinear verification for uniform programs
• Aurora (BCRSVW18)
  • general circuits, $O(\log^2 n)$ arg size
  • linear verification time

Interactive linear PCPs?

Linear IOPs (each round send linear PCP oracle, linear queries to prior oracles sent).

leading to $\rightarrow$ poly IOPs.

$(\mu, d)$ polynomial PCP

• pf $\pi$ is a degree d polynomial $f: \F^\mu \rightarrow \F$
• verifier oracle query $q \in \F^\mu$ returns $f(q)$.

• coordinate queries (i.e., read coefficient of $\pi$?)

Generic reduction: replace coordinate query with 2-round polynomial IOP.

$$\{ \text{point IOPs} \} \subset \{\text{polynomial IOPs} \} \subset \{\text{linear IOPs}\}.$$

SNARKS from polynomial commitments: arithmetic circuit -> constraint system, polynomial testing -(using polynomial commitments)-> interactive argument -(fiat-shamir / hashing)-> non interactive proof.

IOPs with Preproc: in a setup phase, a preprocessor outputs several oracles. Any verifier can read the whole oracle to check its correctness. During ‘online’ interaction with prover, it may make queries to the preprocessed code.

Polynomial IOPs

Informally, PIOP efficiency and security: In a PIOP for NP relation $R$ with arithmetic complexity $n$ (size of the circuit computing $R$):

• verifier runs in time $O(|x|)$
• oracles have degree $O(n)$
• prover honest and $(x,w) \in R \implies$ verifier always accepts
• if $(x,w) \notin R$ and prover does not ‘know’ any witness $w'$ such that $(x,w') \in R \implies$ verifier rejects with overwhelming probability
  • i.e., accept with probability at most $O(\text{poly}(|x|) / | \F |).$

PIOP not used in practice.

*PLONK: There exists a 3 round polynomial IOP for any NP relation $R$ (with arithmetic circuit complexity $n$) with:

• 2 preproccessed oracles, univariate degree $3n$
• 3 online oracles (degree $3n$)
• 5 queries with nonzero outputs
• 8 queries overall

Constraint systems

Recall arithmetic circuits (one kind of constraint system). New: PLONK, R1CS.

Arithmetic Circuit to R1CS

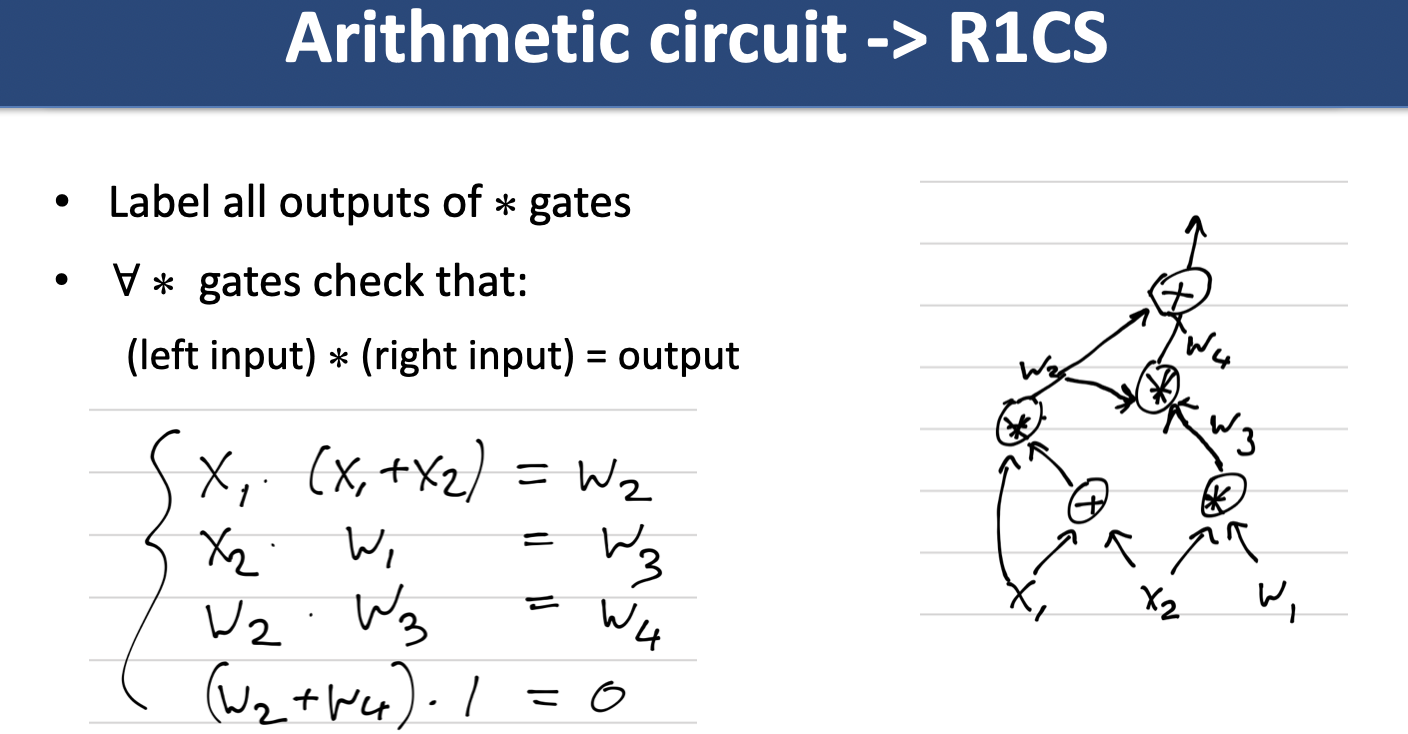
PLONK

11. R1CS Linear IOP to SNARK

Recap on compilation paradigms:

• interactive oracle proofs (IOP)
  • compile with Merkle trees + Fiat-Shamir/RO hash
• polynomial IOP
  • compile with polynomial commitments
• linear IOPs
  • compile with linear only encodings

R1CS to Linear PCP

We have matrices $A, B, C \in \F^{m \times (n+1)}$ and $z = (1,x,w) \in \F^{n+1}.$ Define degree $m-1$ polynomial $f(X)$ by interpolating $f(i) = (A \cdot z)_i.$ Define degree $m-1$ polynomial $g(X)$ by interpolating $g(i) = (B \cdot z)_i$. Define degree $2m -2$ polynomial $h(X)$ as interpolation of $h(i) = (C \cdot z)_i$ for $i \leq m$ and $h(i) = f(i) g(i)$ for $i = m+1, ..., 2m-1$.

Idea: if $h = f \cdot g$ then $(A \cdot z) \circ (B \cdot z) = C \cdot z$ ($\circ$ is Hadamard/comp-wise product). If prover is honest, then $h= f \cdot g$ as defined above. Linear PCP verifier “checks” $h(r) = f(R) g(r)$ at random $r$ implies $h = f \cdot g$ with probability $1 - \frac{2m}{| \F |}.$

12. LPCP to SNARK and HVZK

Linear PCP to SNARK

• trusted party runs $G(A,B,C)$:
  • choose secret random $r \leftarrow \F$
  • $S_V \leftarrow Enc(q_1^L), Enc(q_2^L), Enc(q_3^L)$ (encode individual comps)
  • $S_P \leftarrow Enc(q_1^R), Enc(q_2^R), Enc(q_3^R)$ (encode invididual comps)

Idea: prover can only output encodings of linear transformations of queries:

$$[a] = Enc(<q_1^R, w_1>),[b] = Enc(<q_2^R, w_2>), [c] = Enc(<q_3^R, w_3>).$$

Verifier can check that $a \cdot b = c$ using QuadTest. Remaining issue: how to force prover to use the same $w_1, w_2, w_3$?

Solution: add one more query that does a random linear check:

• choose random $\alpha, \beta, \gamma$
• query for $d = <q^*, w>$ where $q^* = \alpha q^R_1 + \beta q_2^R + \gamma q_3^R$
• check that $d = \alpha a + \beta b + \gamma c$

Prover forced to choose $w_1, w_2, w_3$ independently of the secret $\alpha, \beta, \gamma$.

Summary:

R1CS to linear PCP (previous)

then linear PCP to SNARK:

• trusted setup S forms the LPCP queries and encodes them
• SNARK prover forced to output affine linear transformations of queries
• extra query forces prover to apply same linear transformation to each query

Proof is 4 elements, verifier does two QuadTests.

ZK Linear PCP

A linear PCP for a R1CS program $(A,B,C)$ is zero knowledge if there exists a simulator Sim that takes an input $xx$ and verifier program $V'$ satisfying the following:

For all $x \in \F^{n_1}$ such that $\exists w \in \F^{m-n_1}$ such that program accepts $(x,w)$ and all verifiers V’ making querires M’, Sim outputs:

$$Sim(x,V') \rightarrow (S_P^*, S_V^*, v^*)$$

a random variable distributed identically to $(S_P, S_V, M'_\pi)$ from

$$(S_P, S_V) \leftarrow S(A,B,C)$$

and $\pi \leftarrow P(S_P, x,w)$.

Honest Verifier Zero Knowledge

HVZK for LPCP: assume verifier follows the protocol, then Sim produces output $(S_P^*, S_V^*, v^*)$ which is distributed identically to $(S_P, S_V, M\pi).$

In transformation to SNARK, our trusted setup selects the query vectors honestly.

R1CS to HVZK LPCP

• Prover samples random $\delta_1, \delta_2$
• interpolate $f', g'$ at one more point: $f'(0) = \delta_1, g'(0) = \delta_2$
• $h'(0) = f'(0)g'(0) = \delta_1 \delta_2$
• $f', g'$ are degree $m$ each and $h$ is degree $2m$
• R1CS constraint equation still equivalent to $h'(i) = f'(i)g'(i)$ for $i=1, ..., m$, thus implied by $h' = f' \cdot g'$
• why ZK? queries reveal no more than $f'(r)$ and $g'(r)$ at secret point. These are independent and unfiromly distributed if $r \notin \{1, ..., m\}:$

$$f'(X) - f(X) = \alpha \prod_{i \in [1,m]}(X-i)$$

implies

$$\alpha = \frac{\delta_1 - f(0)}{(-1)^m m!}$$

(independent, uni random). Also,

$$f'(r) = f(r) + \alpha \prod_i (r-i).$$

13. Polynomial IOP for PLONK Constraints

Construction roadmap:

• arithmetic circuit to
• constraint system to
• polynomial IOP to (via polynomial commitment)
• interactive argument to (Fiat Shamir)
• SNARK

Arithmetic Circuit to Constraints

The input is a 2-fan-in arithmetic circuit with $n$ arithmetic gates and $m$ input/output wires. There are $\ell$ public I/O wires. Any circuit can be padded with dummy I/O inputs so that $\ell = 0$ mod $3$. Construct $(s, \sigma, n, m, \ell):$

• Associate the indices $\{3i: i \in [n]\}$ to gate left-input values, $\{3i+ 1: i \in [n]\}$ to gate right-input values, $\{3i +2: i \in [n]\}$ to gate output values, and $\{3i + i: i \in [n]\}$ with the public I/O wires.
• Encode gates: set $s_i =1$ if the $i$-th gate is multiply, else $s_i = 0$ if $i$-th gate is add.
• Encode wiring by defining the permutation $\sigma: [3n+\ell] \rightarrow [3n + \ell]$ as a composition of cycles.

The permutation places toggether in cycles all indices assigned to left-input, right-input, output, and circuit I/O values that are equal according to the wiring.

$x \in \F^\ell$ and $w \in \F^{3n+\ell}$ satisfy this constraint system iff the $w$’s are valid assignments to the $i$-th gate’s left/right/output values for all $i \in [0, n)$ AND the first $\ell$ public I/O values of the circuit are $x_0, ..., x_{\ell -1},$ equal to $w_{3n},..., w_{3n + \ell -1}.$

Constraints to Poly IOP

There’s a lot… Interpolating degree $n = 3n + \ell$ polynomial (selection polynomial), assignment polynomial, permutation polynomial.

Strawman polynomial IOP and efficient permutation argument. Permutation poly IOP, combined poly IOP, linearization optimization.

14. Polynomial IOP for PLONK Constraints, Cont.

Recap: Construction roadmap (arithmetic circuit -> constraint system -> polynomial IOP -(via polynomial commitment)-> interactive argument -(Fiat Shamir)-> SNARK).

Complete SNARK for Polynomial Constraints

Polynomial Commitment

Input: $f(x) \in \F_p(X)$ degree at most $d$.

• Setup($1^\lambda$) $\rightarrow pp$
• Commit($pp, f$) $\rightarrow (c,r)$ for $|c| << d$, ideally $O(\lambda).$
• Open($pp, c, r, f$) $\rightarrow b \in \{0,1\}$

Public coin interactive protocol (communication sublinear in $d$):

• Eval($pp, c, z, y, d; f$)

Commitment is binding and evaluation is binding/argument of knowledge.

Compiling PIOP with Poly Commit

• Prover replaces each oracle $f$ of degree $d$ with a commitment $C_f \leftarrow \text{Commit}(pp,f)$
• For each query $z$ to $f$:
  • Prover sends $y \leftarrow f(z)$
  • Prover/Verifier run Eval($pp, C_f, z, y, d;f)$

Polynomial Commitments

• Several options:
  • Bilinear group based, trusted setup
  • DARK w/RSA, trusted setup
  • DARK w/class groups, no trusted setup
• All of these commitment schemes are additively homomorphic

In an additive (homomorphic) polynomial commitment scheme, $C_f + C_g = C_{f+g}.$ An additive polynomial commitment scheme can compile any Poly IOP to an argument with just 1 Eval execution.

PCS Batch Opening

Generic optimization for opening at multiple points with homomorphic polynomial commitments:

• Given $\{x_i, y_i\}_{i \in [k]}$ let $Z = \prod_{i \in [k]} (X-x_i)$ and $Y(x_i) = y_i$ degree $k$. For $i \in [k], f(x_i) = y_i$ iff there exists $T(X)$ such that $T(X)Z(X) = f(X) - Y(X)$.
• To open the commitment $C$ at points $\{x_i\}$ to $\{y_i = f(x_i)\}$ output commitment $C_T$ to quotient $T(X)$, derive/receive challenge $r \in \F,$ derive $C^*$ commitment to $f^*(X) \leftarrow f(X) - Y(r) - Z(r)T(X)$, and open $C^*$ at point $r$ to show $f^*(r) = 0.$
• Verifier uses homomorphism to derive $C^*$ from $C$ and $C_T$.

This generalizes to multiple polynomials at multiple points. Given $\{C_i\}$ commits to $\{f_i\}$ and ParseError: KaTeX parse error: Expected 'EOF', got '}' at position 17: …{x_{ij}, y_{ij}}̲_{i \in [k], j … for $i\in [k]$:

• Let $Z_i(X) = \prod_{j \in [k_i]} (X-x_{ij}), Z(X) = \prod_{i \in [k]} Z_i(X)$ and interpolate $Y_i(x_{ij}) = y_i.$ Define $\bar Z_i(X) = Z(X) / Z_i(X).$
• Let $\Delta_i(X) = f_i(X) - Y_i(X).$ Note that $f(x_{ij}) = y_{ij}$ iff $Z(X)$ divides each $\bar Z_i(X)\Delta_i(X).$
• To open $\{C_i\},$ derive/receive first challenge $\alpha \in \F$, compute quotient $T(X) = \sum_{i \in [k]} \alpha^i \bar Z_i(X) \Delta_i(X) / Z(X)$. Output commitment $C_T$ to $T(X)$.
• Derive/receive second challenge $r \in F.$ Derive $C^*$ commitment to $f^*(X) \leftarrow \sum_{i \in [k]} \alpha^i \bar Z_i(r)(f_i(X) - Y_i(r)) - Z(r)T(X)$ and open $C^*$ at point $r$ to show $f^*(r) = 0.$

Kate Batch Opening

Special case of Kate PCS: batch opening only 1 group element.

• Pairing $e: G_1 \times G_2 \rightarrow G_T$
• crs = $(g_1, g_1^S, g_1^{s^2}, ..., g_1^{s^d}, g_2, g_2^s, ..., g_2^{s^d})$ for $g_1 \in G_1, g_2 \in G_2.$
• $C_i = \prod_{j \in [d]}g_1^{s^jf_{ij}} = g_1^{f_i(s)}$
• To batch open $\{C_i\},$ derive/receive challenge $\alpha \in \F,$ compute quotient $T(X) = \sum_{i \in [k]} \alpha^i \bar Z_i(X) / Z(X).$ Output commitment $C_T = g_1^{T(s)}.$
• Verifier derives $\forall i$: $g_1^{\alpha^i \Delta_i(s)} = (C_i / g_1^{Y_i(s)})^{\alpha^i}$ and $g_2^{\bar Z_i(s)}.$ Verifier checks the pairing equation $\prod_i e(g_1^{\alpha^i \Delta_i(s)}, g_2^{\bar Z_i(s)}) = e(C_T, g_2^{Z(s)}).$

Final SNARK Size

• 3 Commitments for $f(X), \Sigma(X), Q(X)$ (3 group elements)
• $f(\beta), f(\beta g), f(\beta g^2), \Sigma(\beta), \Sigma(\beta g)$ (5 field elements)
• Opening $f, \Sigma, \bar Z_1, \bar Z_2,$ and linear comb of $S(X), P_{\sigma}(X), Q(X)$ using Eval optimization for multiple polynomials at multiple points
  • 1 group element (less efficient verifier)
  • 2 group elements (more eff. ver.)

Total size: 4-5 group elements, 5 field elemnts

Original PLONK size: 7 group elements, 7 field elements