<-- back to all linear algebra notes

Notes on Linear Algebra Done Right

note: incomplete and may never be finished. also the formatting is bad because i just ripped this off of my notion

Chapter 1—Vector Spaces

1A

• Definition of complex numbers, sets, tuples
• $F$ stands for $\mathbb{R}$ or $\mathbb{C}$ (fields)
• $F^n$ defined as set of all lists of length $n$

1B Definition of Vector Spaces

• Vector space is a set $V$ with addition and scalar multiplication defined s/t:
  • addition commutes + associative
  • additive & multiplicative id.
  • additive inverse
  • distributive property
• If $S$ a set, $F^S$ the set of functions from $S$ to $F$ & is a vector space
• Additive id. and inv. in v.s. are unique
• $V$ denotes a vector space over $F$

1C Subspaces

• $U\subset V$ a subspace of $V$ is $U$ a vector space with the same additive id. and operations as on $V$.

  • In other words, iff $U$ satisfies $0 \in U$, closure under addition, and closure under scalar mult

• Sum of subspaces: for $V_1, …, V_m$ subspaces of $V$,

  $V_1 + … + V_m = \{v_1 + … + v_m : v_1 \in V_1, …, v_m \in V_m \}.$

  and is the smallest subspace of $V$ containing $V_1, …, V_m$.

• For $V_1, …, V_m$ subspaces of $V$,

  $V_1 + … + V_m$ a direct sum if each element can be written in only one way as a sum $v_1 + … + v_m$ where each $v_k \in V_k$, then denoted as $V_1 \oplus … \oplus V_m$

  Direct sum iff the only way to write 0 as a sum $v_1 +…+v_m$ is by taking each $v_k = 0$

• Suppose $U, W$ subspaces of $V$. Then $U + W$ a direct sum $\iff$ $U \cap W = \{0\}$.

Chapter 2—Finite Dimensional Vector Spaces

2A Span and Linear Independence

• Defines linear combination, span
• Span of a list of vectors in $V$ is the smallest subspace of $V$ containing all vectors in the list.
• Vector space is finite dimensional if some list of vectors in it spans the space
• Defines polynomials over $F$, $\mathcal{P}(F)$, and polynomials of degree at most $m$ over $F$, $\mathcal{P}_m(F)$.
• A vector space is infinite dimensional if it is not finite dimensional.
• A list of vectors in $V$ is linearly indepedent if the only choice of $a_1, …, a_m \in F$ s/t $a_1 v_1 + … + a_m v_m = 0$ is $a_1 = … = a_m = 0$
• Suppose $v_1, …, v_m$ linearly dependent in $V$. Then there exists $k \in \{1, 2…, m\}$ s.t. $v_k \in \text{span}(v_1, …, v_{k-1})$.
  • If the k-th term removed from $v_1, …, v_m$, then the span of the remaining list equals the span of the original list
• Every subspace of a finite dimensional vector space is finite dimensional

2B Bases

• Defines basis
• A list $v_1, …, v_n$ of vectors in $V$ is a basis of $V$ iff every $v \in V$ can be written uniquely in the form $v = a_1 v_1 + … + a_n v_n$, where $a_1, …, a_n \in F$.
• Every spanning list contains a basis
• Every finite dimensional vector space has a basis
• Every linearly independent list of vectors in a finite dimensional vector space can be extended to a basis of the vector space
• Every subspace of $V$ is part of a direct sum equal to $V$.
  • e.g., sps. $V$ finite dimensional and $U$ a subspace of $V$. Then there exists a subspace $W$ of $V$ s.t. $V = U \oplus W$.

2C Dimension

• Any two bases of a finite dimensional vector space have the same length
• Dimension of a finite-dimensional vector space is the length of any basis of the vector space, denoted $\text{dim}(V)$
• Dimension of a subspace of a finite dimensional vector space is less than that of the original vector space
• $V$ finite dim. v.s. Then every linearly ind. list of vectors in $V$ of length $\text{dim}(V)$ is a basis of $V$.
• $V$ finite dim v.s. and $U$ a subspace of $V$ s.t. their dimensions are equal. Then $V = U$.
• Every spanning list of vectors of $V$ of length $\text{dim}(V)$ is a basis of $V$
• If $V_1, V_2$ are subspaces of a finite dim v.s., then $\text{dim}(V_1 + V_2) = \text{dim}V_1 + \text{dim}(V_2) - \text{dim}(V_1 \cap V_2)$.

Chapter 3—Linear Maps

3A Vector Space of Linear Maps

• Definition of a linear map:
  • a linear map from $V$ to $W$ is a function $T: V \mapsto W$ with the following properties:
    • additivity: $T(u+v) = T(u) + T(v)$ for all $u,v\in V$
    • homogeneity: $T(\lambda v) = \lambda (Tv)$ for all $\lambda \in F$ and all $v \in V$
• Set of linear maps from $V$ to $W$ denotes $\mathcal{L}(V,W)$
  • from $V$ to $V$ is $\mathcal{L}(V)$
• Suppose $v_1, …, v_n$ a basis of $V$ and $w_1, …, w_n \in W$. Then there exists a unique linear map $T: V \mapsto W$ such that $Tv_k = w_k$ for each $k = 1, …, n$.
• Linear maps are closed under addition and scalar multiplication (i.e., summing two linear maps is still a linear map) defined as
  • $(S+T)(v) = Sv + Tv, (\lambda T)(v) = \lambda (Tv)$
• $\mathcal{L}(V,W)$ is a vector space with the operations defined above

3B Null Spaces and Ranges

• For $T \in \mathcal{L}(V,W),$ the null space of $T$ is the subset of $V$ whose vectors map to 0 under $T$:
  • $\text{null}T = \{v \in V : Tv=0\}$
• Null space is a subspace (above, null T is a subspace of V)
• A function $T: V \mapsto W$ is injective if $Tu = Tv \implies u = v$
• $T \in \mathcal{L}(V,W)$. Then $T$ injective iff $\text{null}(T) = \{0\}$.
• For $T \in \mathcal{L}(V,W),$ the range of $T$ is the subset of $W$ that are equal to $Tv$ for some $v\in V$:
  • $\text{range}(T) = \{Tv : v \in V\}$
• The range is a subspace (above, range T is a subspace of W)
• A function $T: V \mapsto W$ is surjective if its range equals $W$
• Fundamental theorem of linear maps
  • sps. $V$ finite dimensional and $T \in \mathcal{L}(V,W)$. Then $\text{range}(T)$ is finite dimensional and $\text{dim}V = \text{dim null}(T) + \text{dim range}(T)$.
• Sps. $V,W$ finite dim. v.s. s.t. dim V > dim W. Then no linear map from $V$ to $W$ is injective.
• A homogeneous system of linear equations with more variables than equations has nonzero solutions
• A system of linear equations with more equations than variables has no solution for some choice of the constant terms

3C Matrices

• Definition of a matrix
• Definition of matrix of a linear map:

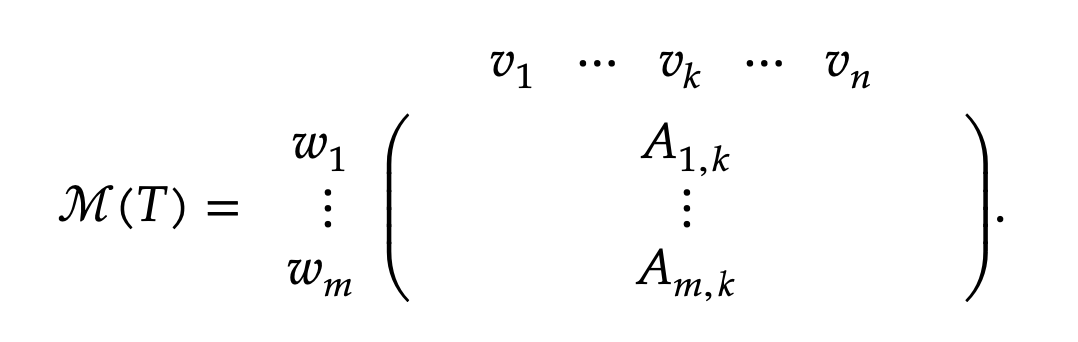
• If $T$ is a linear map from $F^n$ to $F^m$, assuming standard bases, we can think of elements of $F^m$ as columns of $m$ numbers and the k-th column of $\mathcal{M}(T)$ as $T$ applied to the k-th standard basis vector

• For the rest of the section: assume $U,V,W$ finite-dim. and with a chosen basis

  • Defines matrix addition
    • In particular, matrix as the sum of linear maps:
      • $S,T \in \mathcal{L}(V,W)$. Then $\mathcal{M}(S+T) = \mathcal{M}(S) + \mathcal{M}(T)$.
  • Defines scalar multiplication of matrix
    • Similarly as scalar times linear map:
      • $T \in \mathcal{L}(V,W)$ and $\lambda \in F$. Then $\mathcal{M}(\lambda T) = \lambda \mathcal{M}(T)$.
  • Notation: for $m,n$ positive integers, the set of all $m \times n$ matrices with entries in $F$ denoted as $F^{m,n}$
    • With addition and scalar multiplication defined as above, $F^{m,n}$ a vector space of dimension $mn$.

• Defines matrix multiplication

  • Motivation: matrix as product of linear maps
    • If $T \in \mathcal{L}(U,V)$ and $S \in \mathcal{L}(V,W)$, then $\mathcal{M}(ST) = \mathcal{M}(S)\mathcal{M}(T)$
    • (Can use this motivation for understanding when matrices commute, when function composition retains certain properties)
  • Ways to think about matrix product entries:
    • entry in row $j$, column $k$ of $AB$ is row $j$ of $A$ times column $k$ of $B$
    • column $k$ of $AB$ equals $A$ times column $k$ of $B$
    • if $A$ is $m \times n$ and $b$ is $n \times 1$ with entries $b_1, …, b_n$,

      • $Ab = b_1 A_{. , 1} + … + b_n A_{. , n}$

      • i.e., a linear combination of the columns from $A$ and the entries in $b$

        

• Column-row factorization & rank of matrices

  • Definition of column and row rank:
    • $A$ a $m \times n$ matrix with entries in $F$
      • Column rank is dimension of the span of the columns of $A$ in $F^{m,1}$ (e.g., at most $n$)
      • Row rank is dimension of span of the rows of $A$ in $F^{1,n}$ (e.g., at most $m$)
  • Definition of matrix transpose
  • Column-row factorization:
    • Suppose $A$ is $m \times n$ matrix with entries in $F$ and column rank $c \geq 1.$ Then there exists an $m \times c$ matrix $C$ and a $c \times n$ matrix $R$, both with entries in $F$, such that $A = CR$.
      • Pf. Each column of $A$ a $m \times 1$ matrix. The list of columns of $A$ can be reduced to a basis of the span of the columns, a list with length $c$. These $c$ columns in the basis can be put together to form $C_{m \times c}$. Column $k$ of $A$ is a linear combination of the columns of $C$. Make the coefficients of this linear combination into column $k$ of a $c \times n$ matrix, which we call $R$. Then $A = CR$.
    • Column rank = row rank = rank of a matrix

3D Invertibility and Isomorphisms

• Defines invertible, inverse:
  • A linear map $T \in \mathcal{L}(V,W)$ is invertible if there exists a linear map $S \in \mathcal{L}(W,V)$ such that $ST$ equals the identity operator on $V$ and $TS$ equals the identity operator on $W$.
  • A linear map $S \in \mathcal{L}(W,V)$ satisfying $ST = I$ and $TS = I$ is called an inverse of $T$
  • An invertible linear map has a unique inverse
• Invertibility $\iff$ injectivity and surjectivity
• Sps. $V, W$ are finite-dim v.s. with dim $V$ = dim $W$ and $T \in \mathcal{L}(V,W)$.
  • Then $T$ invertible $\iff$ $T$ injective $\iff$ $T$ surjective.
  • Sps also that $S \in \mathcal{L}(W, V)$. Then $ST = I \iff TS = I$.
• An isomorphism is an invertible linear map.
  • Two finite-dim vector spaces are called isomorphic if there is an isomorphism from one vector space onto the other one
• $\mathcal{L}(V,W) \cong F^{m,n}$
• dim $\mathcal{L}(V,W)$ = (dim $V$)(dim $W$)
• Linear maps thought of as matrix multiplication
  • Matrix of a vector:
    • sps. $v \in V$ and $v_1, …, v_n$ a basis of $V$. Then the matrix of $v$ w.r.t. this basis is the $n \times 1$ matrix $\mathcal{M}(v) = \begin{pmatrix} b_1 \\ . \\ . \\ . \\ b_n \end{pmatrix}$, where $b_1, …, b_n$ are scalars s.t. $v = b_1 v_1 + … + b_n v_n$
  • $\mathcal{M}(T)_{.,k} = \mathcal{M}(Tv_k)$ (if we have a linear map from $V$ to $W$, each v.s. with chosen basis, thten the k-th column of $\mathcal{M}(T)$ equals $\mathcal{M}(Tv_k)$
    • e.g. each column of linear map represented as a matrix is the linear map’s action on the corresponding basis vector in the domain, represented as a matrix
  • Hence linear maps act like matrix multiplication:
    • Suppose $T \in \mathcal{L}(V,W)$ and $v \in V$. Suppose $v_1, …, v_n$ basis for $V$ and $w_1, …, w_m$ a basis for $W$. Then $\mathcal{M}(Tv) = \mathcal{M}(T) \mathcal{M}(v)$.
      • Pf. Sps. $v = b_1 v_1 + … + b_n v_n$, with coefficients in $F$. Then $Tv = b_1 Tv_1 + … + b_n Tv_n$ (by linearity). Hence $\mathcal{M}(Tv) = b_1 \mathcal{M}(Tv_1) + … + b_n \mathcal{M}(Tv_n)$ (from the above). This equals $b_1 \mathcal{M}(T)_{.,1} + … + b_n \mathcal{M}(T)_{.,n} = \mathcal{M}(T)\mathcal{M}(v)$, as desired.
  • Sps. $V, W$ are finite-dim and $T \in \mathcal{L}(V, W)$. Then dim range $T$ equals the column rank of $\mathcal{M}(T)$.
    • Pf. Sps. $v_1, …, v_n$ a basis of $V$ and $w_1, …, w_m$ a basis of $W$. The linear map that takes $w \in W$ to $\mathcal{M}(w)$ is an isomorphism from $W$ onto the space $F^{m,1}$. The restriction of this isomorphism to range $T$ is an isomorphism from range $T$ onto span$(\mathcal{M}(Tv_1), …, \mathcal{M}(Tv_n))$. The $m \times 1$ matrix $\mathcal{M}(Tv_k)$ equals column $k$ of $\mathcal{M}(T)$.
• Change of basis
  • Defines identity matrix
  • Defines invertible matrices (matrix inverse not introduced with det / computational method)
  • Suppose $T \in \mathcal{L}(U,V)$ and $S \in \mathcal{L}(V, W)$. If $u_1, …, u_m$ a basis of $U$ and $v_1, …, v_n$ a basis of $V$ and $w_1, …, w_p$ a basis of $W$, then $\mathcal{M}(ST, (u_1, …, u_m), (w_1, …, w_p)) = \mathcal{M}(S, (v_1, …, v_n), (w_1, …, w_p))\mathcal{M}(T, (u_1, …, u_m), (v_1, …, v_n))$.
    • Essentially same result of linear map and matrix mult., with explicit bases
  • Suppose $u_1, …, u_n$ and $v_1, …, v_n$ are bases of $V$. Then the matrices $\mathcal{M}(I, (u_1, …, u_n), (v_1, …, v_n))$ and $\mathcal{M}(I, (v_1, …, v_n), (u_1, …, u_n))$ are inverses of each other
  • Change of basis formula:
    • Shorthand notation: $\mathcal{M}(T, (u_1, … u_n)) = \mathcal{M}(T, (u_1, …, u_n), (u_1, …, u_n))$
    • Sps. $T \in \mathcal{L}(V)$. Sps $u_1, …, u_n$ and $v_1, …, v_n$ are bases of $V$. Let $A = \mathcal{M}(T, (u_1, …,u _n))$ and $B = \mathcal{M}(T, (v_1, …, v_n))$ and $C = \mathcal{M}(I, (u_1, …, u_n), (v_1, …, v_n))$. Then $A = C^{-1}BC$.
  • Suppose $v_1, …, v_n$ a basis of $V$ and $T \in \mathcal{L}(V)$ invertible. Then $\mathcal{M}(T^{-1}) = (\mathcal{M}(T))^{-1}$, where both matrices are w.r.t. basis $v_1, …, v_n$.

3E Products and Quotients of Vector Spaces

• Product of vector spaces is a vector space
• Dimension of a product is the sum of dimensions

• Definition of a translate:

• Defines a quotient space:
  • Sps. $U$ a subspace of $V$. Then the quotient space $V/U$ is the set of all translates of $U$. Thus, $V/U = \{v + U : v \in V \}$
• Want this quotient space to be a vector space.
  • Sps. $U$ a subspace of $V$ and $v, w \in V$. Then $v-w \in U \iff v+ U = w + U \iff (v+U) \cap (w+U) \neq \emptyset$
    • e.g., two translates of a subspace are equal or disjoint
  • Defining addition and scalar multiplication on $V/U$:
    • Sps. $U$ a subspace of $V$. Then addition and scalar multiplication defined as:
      • $(v+U)+(w+U) = (v+w) + U$
      • $\lambda(v+U) = (\lambda v) + U$
  • With the operations above $V/U$ is a vector space.
• Defines quotient map:
  • $U$ a subspace of $V$. The quotient map $\pi : V \mapsto V/U$ is the linear map defined by $\pi(v) = v + U$ for each $v \in V$.
• dim $V/U$ = dim $V$ - dim $U$
• Sps. $T \in \mathcal{L}(V, W)$. Define $\tilde{T}: V / \text{null}T \mapsto W$ by $\tilde{T}(v+\text{null}T) = Tv$.
  • $\tilde{T} \circ \pi = T$, where $\pi$ the quotient map of $V$ onto $V / \text{null}T$
  • $\tilde{T}$ is injective
  • range $\tilde{T}$ = range $T$
  • $V / (\text{null}T)$ isomorphic to $\text{range}T$
  • Hence we can think of $\tilde{T}$ as a modified version of $T$, with a domain that produces a 1-1 map.

3F Duality

• A linear functional on $V$ is a linear map from $V$ to $F$ (an element of $\mathcal{L}(V, F)$

• The dual space of $V$, denoted $V’$, is the vector space of all linear functionals on $V$, i.e., $V’ = \mathcal{L}(V, F)$

• Sps. $V$ is finite dimensional. Then $V’$ is also finite-dimensional and dim $V’$ = dim $V$.

  • Pf. dim $V’$ = dim $\mathcal{L}(V,F)$ = dim $V$ dim $F$ = dim $V$.

• If $v_1, …, v_n$ a basis of $V$, then the dual basis of $v_1, …, v_n$ is the list $\phi_1, … \phi_n$ of elements of $V’$, where each $\phi_j$ is the linear functional on $V$ such that

  $$\phi_j(v_k) = \begin{cases} 1 & k=j \\ 0 & k \neq j \end{cases}$$

• The dual basis of a basis of $V$ consists of the linear functionals on $V$ that give the coefficients for expressing a vector in $V$ as a linear combination of the basis vector:

  • Sps. $v_1, …, v_n$ a basis of $V$ and $\phi_1, …, \phi_n$ is the dual basis. Then $v = \phi_1 (v) v_1 + … + \phi_n (v) v_n$ for each $v \in V$.

• For $V$ finite dimensional, the dual basis is a basis of the dual space.

• Sps. $T\in \mathcal{L}(V, W)$. The dual map of $T$ is the linear map $T’ \in \mathcal{L}(W’, V’)$ defined for each $\phi \in W’$ by $T’(\phi) = \phi \circ T$.

CH. 3 NOT DONEEEE

Chapter 5—Eigenvalues and Eigenvectors

Standing notation: $F$ is the reals or the complex numbers, $V$ is a vector space over $F$

Eigenvalues

• A linear map from a vector space to itself is called an operator

• $T \in \mathcal{L}(V)$. A subspace $U$ of $V$ is called invariant under $T$ if $Tu \in U$ for every $u \in U$

  • Motivation: to understand the behavior of a linear operator, we only need to understand the behavior of the linear operator restricted to subspaces which partition the entire $V$. However, to apply many useful tools, we want the restriction of T to a subset (say, $V_k$) to map back into $V_k$, hence we would like to study invariant subspaces

  • Thus $U$ is invariant under $T$ if $T|_u$ is an operator on $U$

    

• The simplest possible nontrivial invariant subspaces (other than $\{0\}$ and $V$) are invariant subspaces of dimension 1.

  • Take any $v \in V$ with $v \neq 0$ a nd let $U = \{\lambda v : \lambda \in F \} = \{\text{span}(v)\}$. $U$ is a 1 dimensional subspace of $V$ (and every 1-dimensional subspace of $V$ is of this form for some appropriate $v$).
  • If $U$ is invariant under an operator $T \in \mathcal{L}(V)$, then $Tv \in U$, and so there exists a scalar $\lambda \in F$ such that $Tv = \lambda v$.
  • Conversely, if $Tv = \lambda v$ for some $\lambda \in F$, then $\text{span}(v)$ is a 1-dimensional subspace of $V$ invariant under $T$.

• $T \in \mathcal{L}(V)$. A number $\lambda \in F$ is an eigenvalue of $T$ if there exists $v \in V$ such that $v \neq 0$ and $Tv = \lambda v$.

  • For an eigenvalue $\lambda$, the corresponding vector $v \in V$ s.t. $Tv = \lambda v$ is an eigenvector

• Every list of eigenvectors corresponding to distinct eigenvalues of $T \in \mathcal{L}(V)$ is linearly independent

• For a finite-dimensional vector space $V$, each operator on $V$ has at most dim(V) distinct eigenvalues